Periodic Table Law:
The modern periodic table, based on atomic number and electron configuration, was created primarily by a Russian chemist, Dmitri Ivanovich Mendeleev, and a German physicist, Julius Lothar Meyer, both working independently. They both created similar periodic tables only a few months apart in 1869.
Mendeleev created the first periodic table based on atomic weight. He observed that many elements had similar properties, and that they occur periodically. Hence, the table’s name.
His periodic law states that the chemical and physical properties of the elements vary in a periodic way with their atomic weights. The modern one states that the properties vary with atomic number, not weight.
Elements in Mendeleev's table were arranged in rows called periods. The columns were called groups. Elements of each group had similar properties.
The Periodic table can also be divided into several families of elements each having similar properties. For our purposes we will define the following ten families:
Alkali metals
The alkali metals, found in group 1 of the periodic table, are highly reactive metals that do not occur freely in nature. These metals have only one electron in their outer shell. Therefore, they are ready to lose that one electron in ionic bonding with other elements. As with all metals, the alkali metals are malleable, ductile, and are good conductors of heat and electricity. The alkali metals are softer than most other metals.
Alkaline earth metals
The alkaline earth elements are metallic elements found in the second group of the periodic table. All alkaline earth elements have an oxidation number of +2, making them very reactive.
The Transition metals
The 38 elements in groups 3 through 12 of the periodic table are called "transition metals." As with all metals, the transition elements are both ductile and malleable, and conduct electricity and heat. Their valence electrons are present in more than one shell. This is why they often exhibit several common oxidation states.
Transition metals have high melting points due to strong metallic bonds. The number of unpaired electrons in the outermost shell will determine the strength of the metallic bonds.
Other metals
The "other metals" (also known as "Post transition metals") elements are located in groups 13, 14, and 15. While these elements are ductile and malleable, they are not the same as the transition elements. These elements, unlike the transition elements, do not exhibit variable oxidation states, and their valence electrons are only present in their outer shell. All of these elements are solid, have a relatively high density, and are opaque. They have oxidation numbers of +3, ±4, and -3.
Metalloids
Metalloids are the elements found between the boundary that distinguishes metals from non-metals. Metalloids have properties of both metals and non-metals. Some of the metalloids, such as silicon and germanium, are semi-conductors.
Non-metals
Non-metals are the elements in groups 14-16 of the periodic table. Non-metals are not able to conduct electricity or heat very well. As opposed to metals, non-metallic elements are very brittle. The non-metals can be gases, such as oxygen and solids, such as carbon. The non-metals have no metallic luster, and do not reflect light. They have oxidation numbers of ±4, -3, and -2.
Halogens
The halogens are five non-metallic elements found in group 17 of the periodic table. All halogens have 7 electrons in their outer shells, giving them an oxidation number of -1. Halogens are strong oxidizing agents as they want to accept electrons. The members of the halogen family go from gas->liquid->solid at room temperature as you descend the group
Noble gases
The noble gases are found in group 18 of the periodic table. These elements have an oxidation number of 0. This prevents them from forming compounds readily. All noble gases have 8 electrons in their outer shell, making them stable and highly non-reactive.
Lanthanide Series
The Lanthanides consist of the elements in the f-block in the sixth period of the periodic table (they donot belong to a group). They are soft metals, all naturally occur except for Promethium
Rare earth elements which are useful for their metallurgical properties are composed of the lanthanide series plus Scandium and Yttrium.
Actinides Series
The Actinides series consist of the elements in the f-block in the seventh period of the periodic table (they donot belong to a group). All the elements of Actinides series are radioactive and most are synthetic, that is, human-made. All have a silvery or silvery-white luster in metallic form.
Periodic Table Trends:
When elements are arranged in order of increasing atomic number, there is a periodic repetition of their physical and chemical properties. Some of these properties include atomic radius, electronegativity, ionization energy and metallic characteristics.
Factors affecting these properties include the number of protons in the nucleus, the distance from the nucleus and amount of shielding inner electrons provide to the valence electrons.
Electron shielding describes the ability of an atom's inner electrons to shield its positively-charged nucleus from its valence electrons. The net effect is that the valence electrons are not bound as tightly to the nucleus as they would be if they were alone.
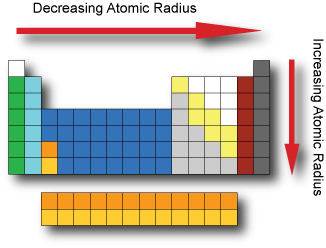
Atomic radius
The atomic radius is a somewhat imprecise measure that can refer to the mean distance from the center of the nucleus to the boundary of the surrounding electron cloud.
We can determine the radius by dividing the distance between two bonded atoms in half. Depending upon the type of bond we can obtain very different values. If the bond is covalent it is called a covalent radius. If the bond is ionic it is called an ionic radius. If the bond is metallic it is called the metallic radius
The Atomic radius tend to decrease when moving across a period from left to right. As we move across a period electrons are added to the same energy level and protons are added to the nucleus; increasing the effective nuclear charge and pulling the electrons closer to the nucleus.
The Atomic radius tend to increase when moving down a group from top to bottom. As we go down a group additional energy levels are added; and each subsequent energy level is further from the nucleus.
The Lanthanide contraction describes the greater than expected decrease in ionic radii of the elements in the lanthanide series. The effect is mostly the results from poor shielding of nuclear charge by the 4f electrons; the 6s electrons are drawn towards the nucleus, resulting in a smaller atomic radius.
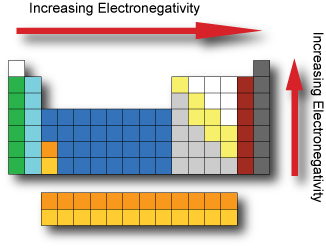
Electronegativity
Electronegativity is the tendency of an atom to attract electrons. It cannot be measured directly and needs to be computed from other atomic properties. The Pauling scale is a dimensionless quantity developed by Linus Pauling used to describe the electronegativity of an atom. The two key factors in determining electronegativity are its atomic number and radius. Fluorine has the highest electronegativity and francium the lowest.
If the electronegativity difference between two atoms is very large, then the bond type tends to be more ionic, if the difference in electronegativity is small then it is a nonpolar covalent bond.
The opposite of electronegativity is electropositivity: a measure of an element's ability to donate electrons.
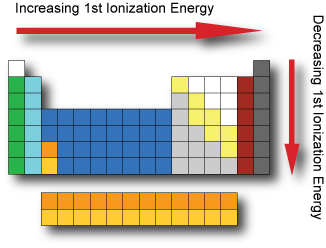
Ionization energy
The ionization energy is the energy it takes to remove an electron from a gaseous neutral atom or ion in it's ground state: X(g) → X+(g) + e-
The highest-energy electron (least tightly bound) is always removed first.
The 1st ionization energy I1 is the energy required to remove an electron from a neutral atom.
The 2nd ionization energy I2 is the energy required to remove an electron from a cation with a +1 charge.
The 3rd ionization energy I3 is the energy required to remove an electron from a cation with a +2 charge.
The increasingly positive charge binds the electrons more tightly; as a result: I1 < I2 < I3
In general, the (n+1)th ionization energy is larger than the nth ionization energy.
In general, the 1st ionization energy increases as we go across a period; as the electrons are held closer to the nucleus with the increasing effective nuclear charge.
In general, the 1st ionization energy decreases as we go down a group; as the electrons are further from the nucleus with each increasing energy level.
The noble gases possess very high ionization energies because their full valence shell makes them highly stable.
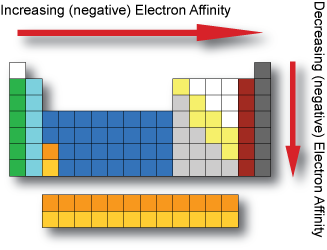
Electron Affinity
Electron affinity is the amount of energy (in KJ/mole) that is released when an electron attaches to a neutral gaseous atom to form an negative ion: X(g) + e- → X-(g)
Electron affinity will be negative (ΔE < 0) when is energy is given off. This indicates that the potential energy of the system is lowered. This stabilizes the system.
A large (negative) electron affinity indicates that the anion is stable. A very small or a positive value indicates that anions do not tend to form.
In general, electron affinity increases (becomes more negative) as we go across a period.
In general, electron affinity decreases (becomes less negative) as we go down a group.
The Noble gases have very small electron affinities; due to their filled valence shells.
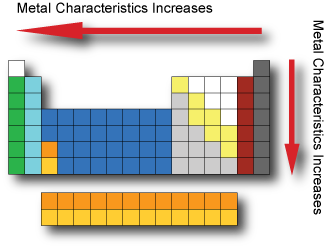
Metal Characteristics
Metals are usually shiny, malleable, hard and are good conductors of electricity and heat.
Metals have low ionization energy and low electronegativity which allows them to conduct electricity as electrons can flow through them easily.
Metal characteristics tend to increase when moving from the top-right to bottom-left of the periodic table.
The most nonmetallic elements(oxygen, fluorine, chlorine) occur at the top right of the Periodic Table.
In general, metals tend to lose electrons to form cations (positively charged ion) and nonmetals tend to gain electrons to form anions (negatively charged ion).
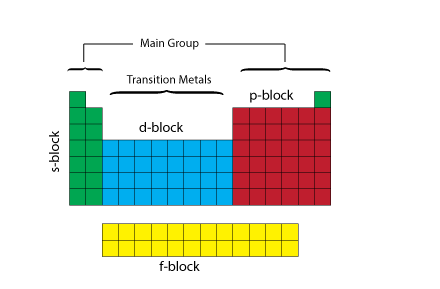
Periodic Table blocks
The periodic table can be divided up into several blocks based on their highest energy electron orbital type.
The s-block consists of the groups 1 and 2 elements plus Helium.
The p-block consists of the groups 13 to 18 elements but not Helium.
The d-block consists of the groups 3 to 12 elements.
The f-block consists of the Lanthanides and Actinides.
We can also divide the table between main group and transition metals. The main group elements include groups 1 and 2 (excluding Hydrogen) on the left of the periodic table and groups 13 to 18 on the right of the table.
The transition metals are the metallic elements that serve as a bridge, or transition, between the two sides (metals and non-metals) of the table. The lanthanides and the actinides at the bottom of the table are sometimes referred to as the inner transition metals.
Atoms and Isotopes
Each element in the periodic table is made up of atoms with the same atomic number (Z). Each atom is composed of a postively charged nucleus (Ze+) and surrounded by electrons with an equal but negative charge (Ze-). The nucleus of an atom is composed of one or more protons and zero or more neutrons.
Protons are elementary particle of matter with a positive charge of +e and a rest mass of 1.673x10-27kg.
Neutrons have no charge and a slightly larger rest mass of 1.675 x 10-27kg.
Electrons are elementary particle of matter with a negative electric charge of -e and a rest mass of about 9.109 × 10–31 kg.
The number of protons in an atom is called the atomic number (Z) and determines which element the atom is. The number of neutrons determines the isotope of the element. The number of neutrons combined with the number of protons is the mass number (A). The mass number is almost equal to the atomic mass. The atomic mass also includes the weight of the electrons in an atom; which have very little mass.
The atomic weight or relative atomic mass is the sum of the products of the relative atomic mass and the mole fraction of each stable and long-lived radioactive isotope of that element in the sample. atomic masses are scaled (expressed relative) to one-twelfth the mass of a carbon-12 atom, atomic weights are dimensionless.
Isotopes are atoms of a chemical element whose nuclei have the same atomic number, Z, but different a Atomic mass. The atom can either be a stable isotope or a radioactive isotope.
A stable isotope is an atom for which no radioactive decay has ever been experimentally measured.
A radioactive isotope (radioisotope) is an atom for which radioactive decay has been experimentally measured
The symbol for an isotope can be represented as:
AXZ or AX or X-A
Where:
X = Chemical Element Symbol
N = number of neutrons
Z = atomic number or number of protons;
A = N+Z
Note: The value of Z is given for a particular element X, so it often left out.
For example Cobalt-60 can be represented as: 60Co27 or 60Co or Co-60
Where: Z = 27 protons, N = 33 neutrons, A= 27+33 = 60
Electron Configuration Notation:
When writing an electron configuration, we first write the energy level (n), then the subshell to be filled (s, p, d or f), and a superscript which is the number of electrons in that subshell.
Each orbital can hold a maximum of two electrons. The s orbital has only 1 type (orientation) and can hold a maximum of 2 electrons, p has three types (maximum 6 electrons), d five types (10 maximum electrons) and f seven types (14 maximum electrons).
For example Helium has an electron configuration of 1s2; the "1" denotes the energy level or shell (also known as the principle quantum number "n") the "s" the type of orbital and the "2" denotes the number of electrons.
Noble gas short form is an abbreviated notation; where the noble gas from the previous period is used to represent inner core electrons.
for example Phosphorus (Z=15) can be written: 1s22s22p63s23p3 or by taking the previous noble gas Neon to represent the inner core electrons as: [Ne]3s23p3
Orbital diagrams are pictorial representations of the electrons in their orbitals. Orbitals are represented by boxes with up to two electrons. The electrons are represented by an up or down arrow to indicate their spin.
For example Boron's (Z=6) orbital diagram is:
Electron Configuration and the Periodic Table
The electron configuration of each element is determined by its position on the periodic table. The energy level is determined by the period and the number of electrons is given by the atomic number of the element.
Note that the energy level (n) is equal to the period number for s and p block elements, for d block elements n = period -1, and for the f-block n = period -2.
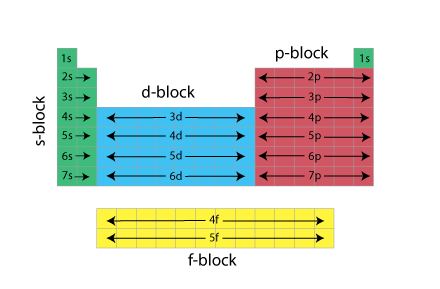
We can use the periodic table to determine the electron configuration of an atom, along with the rules for assigning the electron configuration (Hunds, Pauli...etc.).
Valence electrons
The electrons in the outermost shell are the valence electrons; the electrons in an atom that can be gained or lost in a chemical reaction. Core electrons are the electrons in an atom that are not valence electrons and therefore do not participate in bonding. Since filled d or f subshells are seldom involved in a chemical reaction, we can define valence electrons as follows: The electrons in an atom that are not present in the previous Noble gas, ignoring filled d or f subshells.
The octet rule is a chemical rule of thumb that states that main-group elements tend to combine in such a way that each atom has eight electrons in its valence shell (or two electrons for hydrogen and lithium), giving it the same electronic configuration as the nearest noble gas on the periodic table.
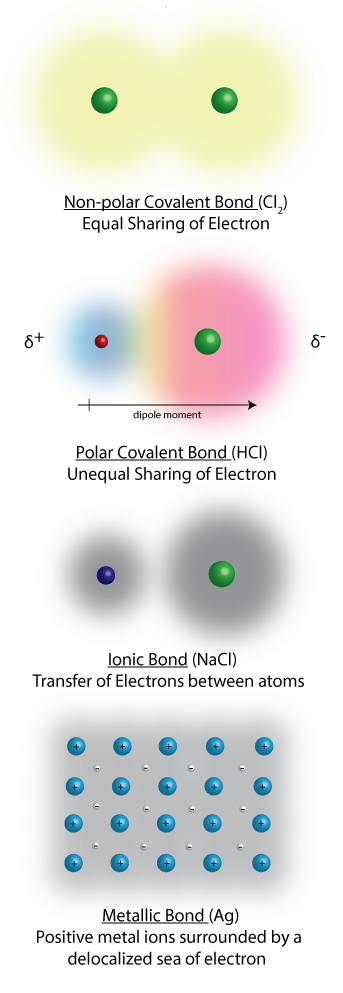
Chemical bonding
The atoms of a compound are held together by chemical bonds formed by the interaction of electrons from each atom. A stable compound occurs when the total energy of the combination has lower energy than the separated atoms. When a bond forms, energy is released. This release of energy shows that the molecule is more stable than the separate atoms.
A covalent bond is formed by two atoms sharing electrons, either equally to yield a nonpolar bond or unequally to form a polar bond. In a polar covalent bond electrons are shared unequally between the two atoms; with the electron density being greater around the more electronegative atom. A covalent bond is formed between two non-metals; where neither atom has a strong enough attraction to pull electrons from the other.
Ionic bond is formed by an almost complete transfer of electrons from one atom to another; resulting the formation of a postively charged and negatively charged ions which are attracted to each other by electrostatic forces. Ionic bonds occur mainly between a metallic and a non metallic atom.
Metallic bonding is the electrostatic attraction between the positively charged atomic nuclei of metal atoms and the delocalized electrons in the metal.
The Oxidation State
The oxidation state, indicates the number of electrons that an atom uses or receives when it forms a compound. The oxidation number will be negative when the atom gains electrons, or shares them with a less electronegative atom. The oxidation number is positive if the atom loses electrons, or shares with a more electronegative atom.
It also determines the ability of an atom to oxidize (to lose electrons) or to reduce (to gain electrons) other atoms or species.
For example Halogens are strong oxidizing agents as they want to accept electrons and Alkali metals are strong reducing agents as they wish to donate an electron.
General rules for oxidation state (Note: these rules must be followed in order):
- For any free element (element not combined with a different element), the oxidation number is zero (example: Fe, H2, He, S8).
- For any neutral compound, the sum of the oxidation numbers must be zero.
- The sum of the oxidation states of all the atoms in an ion is equal to the charge on the ion.
- The oxidation state of group 1 elements is +1, unless in elemental form.
- The oxidation state of group 2 elements is +2, unless in elemental form.
- The oxidation state of fluorine is -1 in all compounds.
- The oxidation state of hydrogen is +1 when combined with a non-metal and -1 when combined with a metal.
- The oxidation state of oxygen is -2 in most compounds, except peroxides (e.g. H2O2) where it is -1.
Quantum mechanics and the periodic table
At the start of the 20th century it was realized that classical Newtonian physics and classical electromagnetic theory could not explain a number of physical phenomena including the photoelectric effect, blackbody radiation and the spectral emission of a hydrogen atom.
To solve the problem of black body radiation, Max Planck proposed that the energy of electromagnetic radiation is not emitted as a unbroken stream but in discontinuous bits or portions; which he termed quanta. He concluded that each quanta carries an amount of energy given by the equation E =hv; where v is frequency and h is Planck's constant (6.626 x 10-34 Joules Sec)
Albert Einstein used a similar assumption to solve the problem of the photoelectric effect; observing that light is quantized and that the energy of light is not transferred continuously as in a classical wave, but only in small "packets" or quanta of light — which are now called photons.
However the Thomas Young's “double-slit” experiment had already shown that light caused interference, a characteristic property of waves. This dual nature of light (electromagnetic radiation); sometimes behaving like a wave and sometimes behaving like a particle depending upon the experiment being performed.
Another important idea in the field of quantum mechanics is the Heisenberg uncertainty principle. The uncertainty principle states that the position and momentum of a particle can never be precisely measured simultaneously. If one is known, the other cannot be determined accurately.
Bohr Model of the Hydrogen Atom
When examining the spectral emission of an excited hydrogen gas; a series of discreet lines are observed instead of a continuous one.
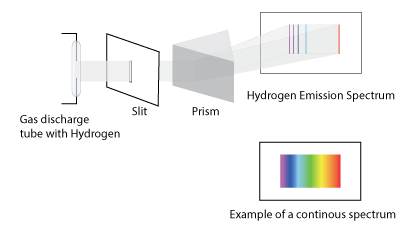
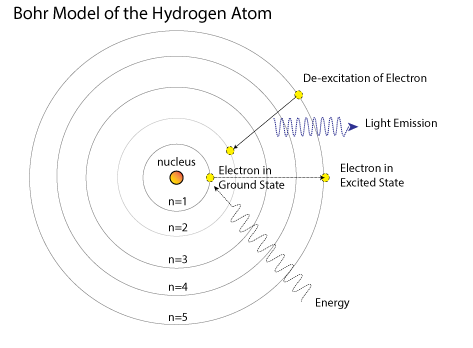
Bohr proposed a model of the hydrogen atom based upon an electron revolving around a nucleus in a stable circular orbit. The only orbits where the electron had a fixed angular momentum equal to nħ were allowed (where ħ = h/2π). He also postulated that electrons can move from one orbit to another by absorbing or releasing discreet (quantized) amount of energy. His model successfully describe the line spectrum of an hydrogen atom. However, it only applied to the hydrogen atom and could not describe atoms with more than 1 electron.
The diagram below shows the bohr model with an electron moving from the ground state after absorbing energy to an excited state. The ground state is defined as the lowest energy state and the excited state is any state with an energy greater than ground state.
de Broglie Matter Waves
Louis de Broglie proposed that if electromagnetic radiation could behave sometimes like a wave and sometimes like a particle, then perhaps a particle like an electron could behave like a wave also. In fact any moving particle, whatever it size, will have wave properties associated with it. These matter waves have a de Broglie wavelength given by:
λ = h/p = h/mv where h = Planck's constant, p = momentum, m= mass, v = velocity.
Schrödinger Wave Equation
Schrödinger extended de Broglie's theory and treated electrons not as particles moving in a well defined orbit, but as a 3-dimensional standing wave system represented by a wave function ѱ, the magnitude of which represents the varying amplitudes of the wave system at various points around the nucleus.
In quantum mechanics, all of the properties of physical objects are described through a wave function, which has a certain value (in general a complex number) at every point in space.
Schrödinger developed partial differential equations for particles which described their quantum mechanical behavior.
The time-dependent one-dimensional Schrödinger equation can be given by:
| ħ |
∂2ѱ(x,t) |
+ V(x,t) ѱ(x,t) = i ħ |
∂ѱ(x,t) |
| 2m | ∂x2 | | ∂t |
where, ѱ is the time-dependent wave function, V is potential energy.
The Schrödinger wave equation does not tell us where an electron is located. But by taking the square of the wave function ѱ2; we are able to find the probability of the electron being present in a volume in space.
To solve the Schrödinger equation for an electron 3 quantum numbers are needed. (n, ℓ, ml ) corresponding to the 3 dimensions in space.
The principal quantum number, "n" can be any positive integer starting at 1. It determines the overall size of the orbital and the energy of the electron. Also referred to as the Shell. The maximum number of electrons a shell can accommodate is given by 2n2 electrons.
The orbital angular quantum number, "ℓ" this defines the shape of the orbital (for s-orbital = 0, p-orbital = 1, d-orbital =2, f-orbital = 3), it has values of 0, 1, 2, ... n-1. Also referred to as the Subshell. The maximum number of electrons that can be placed in a subshell is given by 2(2ℓ + 1).
The magnetic quantum number, " ml" describes the orientation in space of the orbital and has values of -ℓ ...,0,... +ℓ. Also referred to as the orbital. Each orbital can only hold two electrons.
A fourth quantum number, magnetic spin "ms" was added to the electron when it was observed that atomic emission spectral lines are split into multiple lines when an electric field is applied. This number takes into account the magnetic properties of electrons. Although electrons do not actually spin, they do possess a magnetic moment, and can exist in one of two states, spin up ms=+1/2 (displayed as ↑ in an orbital diagram), or spin down ms =-1/2 (displayed as ↓ in an orbital diagram). It is the magnetic moment associated with electron spin that gives all substances their magnetic properties. Substances with all of their electrons paired are slightly repelled by magnetic fields and are said to be diamagnetic. Substances with electrons that have unpaired spins are attracted to magnetic fields and are said to be paramagnetic.
Orbitals:
Atomic Orbitals are regions of space around the nucleus in which there is a high probability of finding an electron. These regions can be obtained by solving the Schrödinger equation for n, ml, ms.
There are 4 types of electron orbitals; "s" which can hold 2 electrons and is spherical in shape, "p" which can hold 6 and is shaped like a dumb-bell, "d" which can hold 10 and is shaped like a clover leaf and "f" which can hold 14.
The shape of any orbital is defined by the nodes. In quantum mechanics a node is a point where an electron cannot exist. There are two types of nodes: angular and radial.
An angular node is usually a planar or conical surface in which there is no electron density.
A radial node appears to be a spherical surface in which there is no electron density
Angular: An atomic orbital will have ℓ angular nodes. So, an s-orbital has 0 a p-orbital has 1, and so on.
Radial: Each atomic orbital will have n-ℓ-1 radial nodes. So a 3s orbital has 3-0-1 = 2 radial node.
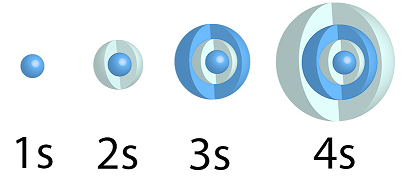
s-orbitals
All s orbitals are spherical; since they have zero angular nodes (ℓ=0 for s-orbitals). The relative sizes of the 1s, 2s, 3s and 4s orbitals are shown below. These figures represent, the boundary surfaces of these orbitals, the volume which contains 90% of the electron density.
n >= 1, ℓ=0, ml=0
The colors correspond to regions of space where the phase of the wave function is positive (dark blue) and negative (pale blue).
In the cut away views of 2s, 3s & 4s locations where the color changes (from a pale to dark blue) are nodal surfaces; where the probabilty of finding an electron are zero.
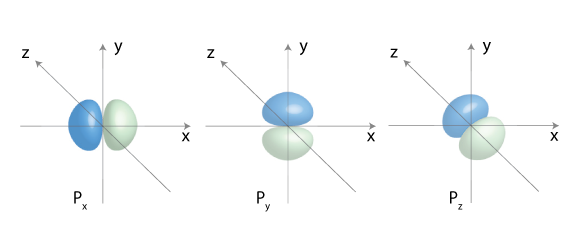
p-orbitals:
There are three p-orbitals px, py and pz
n >=2, ℓ=1, ml={-1, 0, 1}
Here is the 2p orbital:
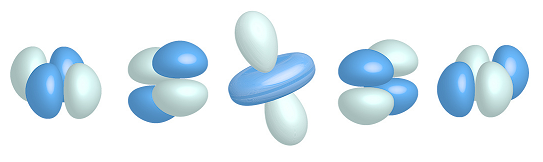
d-orbitals:
There are five d-orbitals
n >= 3, ℓ=2, ml={-2, -1, 0, 1, 2}
Here is the 3d orbital:
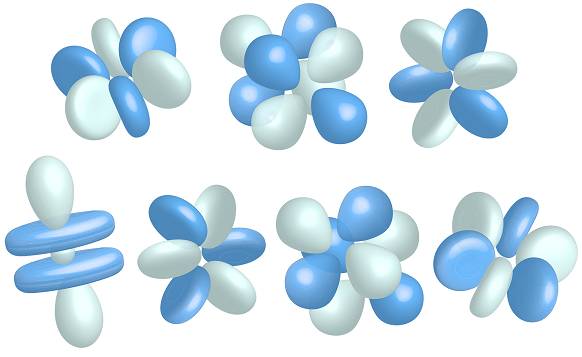
f-orbitals:
There are seven f-orbitals
n >= 4, ℓ=3, ml={-3, -2, -1, 0, 1, 2, 3}
Here is the 4f orbital:
Rules for Assigning Electron Configurations:
According to the Pauli exclusion principle no two electrons in an atom can have the same set of 4 quantum numbers (n, l, ml, ms).
Hund's rule states that even if multiple orbitals of the same energy are available, electrons fill unoccupied orbitals first, before reusing orbitals occupied by other electrons.
For Example: Nitrogen (Z=7), has a configuration: 1s22s22p3
| |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p3 |
Notice that all the electrons have the same +1/2 spin (spin up).
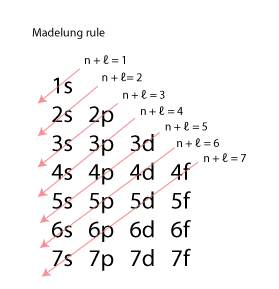
The Aufbau principle (or build-up principle) describes how electrons will be distributed amongst the orbitals. The Aufbau principle states that electrons will fill the lowest available energy levels before filling higher levels (e.g., 1s before 2s).
The order in which these orbitals are filled is given by the n + ℓ rule, also known as the Madelung ordering rule.
Orbitals with a lower n + ℓ value are filled before those with higher n + ℓ values. In the case of equal n + ℓ values, the orbital with a lower n value is filled first.
This gives us a filling order of:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 5d = 4f < 6p < 7s < 6d = 5f
Note: The Madelung ordering rule applies only to neutral atoms in their ground state and even then there are multiple exceptions.
When two electrons occupy the same orbital, they not only have different spins (Pauli exclusion principle), the pairing raises the energy slightly. A half filled subshell and a full filled subshell lower the energy, increasing stability. Due to this and other factors we have the following exceptions to the Aufbau principle.
Some noteable exceptions to Aufbau principle:
Chromium (Cr): [Ar]4s13d5 → s and d subshells are half full.
Molybdenum (Mo): [Kr]4d55s1 → s and d subshells are half full.
Copper (Cu): [Ar]4s13d10 → filled d subshell, leaving s half filled.
Silver (Ag): [Kr]5s14d10 → filled d subshell, leaving s half filled.
Gold (Au): [Xe] 4f145d106s1 → filled d subshell, leaving s half filled.
Palladium (Pd): [Kr] 4d10 → filled d subshell, leaving s empty.
Platinum (Pt): [Xe] 4f146s15d9
Electron Configuration of anions and cations
The electron configuration of anions and cations are assigned in a similiar way to their neutral atoms. Generally following the Pauli exclusion principle, Hund's rule and the Aufbau principle.
For the electron configuration of anions extra electrons are added according to the Aufbau principle. For example: F1- has an electron configuration of [Ne] 2s22p6
For the electron configuration of a cation; electrons are removed first from the outermost highest energy level (n). The effect of this is that for d-block elements the s orbitals are lost first. For example for Zn2+ the electron configuration is: [Ar] 3d10
Ground State Electron Configuration (for first four period of the periodic table):
H (Z=1)
He (Z=2)
Li (Z=3)
Be (Z=4)
B (Z=5)
C (Z=6)
N (Z=7)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p3 |
O (Z=8)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p4 |
F (Z=9)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ |
| |
1s2 |
|
2s2 |
|
2p5 |
Ne (Z=10)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
Na (Z=11)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s1 |
Mg (Z=12)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
Al (Z=13)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
|
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p1 |
Si (Z=14)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p2 |
P (Z=15)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p3 |
S (Z=16)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p4 |
Cl (Z=17)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p5 |
Ar (Z=18)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
K (Z=19)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s1 |
Ca (Z=20)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
Sc (Z=21)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
|
|
|
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d1 |
Ti (Z=22)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
|
|
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d2 |
V (Z=23)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
↑ |
|
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d3 |
Cr (Z=24)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
|
↑ |
↑ |
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s1 |
|
3d5 |
Note that Cr is an exception to Aufbau, here we have an half-filled 3d and 4s subshell; this is a particular stable configuration. Also in the same group Mo (Z=42) will also has a half filled subshell: [kr]5s14d5.
Mn (Z=25)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ |
↑ |
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d5 |
Fe (Z=26)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ |
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d6 |
Co (Z=27)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d7 |
Ni (Z=28)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d8 |
Cu (Z=29)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s1 |
|
3d10 |
Note that Cu is another exception to Aufbau, here we have an filled 3d and a half filled 4s subshell; this is a particular stable configuration. Also in the same group Ag (Z=47), Au (Z=79) will also has a filled d subshell and a half filled s subshell.
Zn (Z=30)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
Ga (Z=31)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
|
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p1 |
Ge (Z=32)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
↑ |
|
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p2 |
As (Z=33)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p3 |
Se (Z=34)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
↑ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p4 |
Br (Z=35)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p5 |
Kr (Z=36)
| |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
↑ ↓ |
|
↑ ↓ |
↑ ↓ |
↑ ↓ |
| |
1s2 |
|
2s2 |
|
2p6 |
|
3s2 |
|
3p6 |
|
4s2 |
|
3d10 |
|
4p6 |
Copyright, Model Science Software, 2017.